About a month ago, I met Joe Palca, NPR science correspondent extraordinaire. He has a series of very short science segments that fill little gaps between other stories, and since these segments fill holes, he decided to make them about holes as well. There was one on what would happen if you could throw a ball through the center of the Earth, another on donuts, and one that asked a philosopher to tell us “What is a hole, really?” – you get the idea. Anyway, through a confluence of circumstances, I teamed up with mutual friends Rachael Porter and Genevieve Jones to make a video that could tie into one of these pieces on holes, and (voilà!) this is what we came up with:
Joe’s piece, which aired this past Tuesday, was about homophones, and his example (going with the theme) was “whole/hole.” Rachael, Gen, and I decided to do something a little different, and we came up with a love story based around a single sentence containing an ambiguous word, “pair.” We wanted to know what has to happen in the brain from the moment you hear a sound that turns out to be words through the moment you understand what the words mean, and our cute, creepy, silly video is our interpretation of what we found when we looked into the literature.
I’m a planet scientist, not a brain scientist, so I’m sure (and the YouTube comments assure me too) that there are some things we could have done differently when it comes to the details of brain functions. My hope is that it’ll reach a broader audience than a lot of the videos I’ve worked on in the past – it’s certainly different! – and encourage people to think about how incredible it is, really, that our brains are constantly interpreting all of the many signals we send it in (essentially) real time.
In any case, though, I wanted to share some of the amazing things I learned about the brain while researching the video. Since this isn’t my field of study, it was pretty tough going through some of the papers (cited below), but it was worth it!
- When you hear spoken words, it takes your brain longer to interpret the ones that have multiple possible meanings (homophones) than to understand the unambiguous ones. Ok, not surprising.
- When you’re reading words on a page, ambiguous words (homonyms) actually have a processing advantage over unambiguous words. WHAT? So interesting.
- Learning to read changes the way your brain processes spoken words by involving the area that controls spelling and visual word images (along with the language comprehension areas). Once you learn to read, your brain is different forever. Whoa.
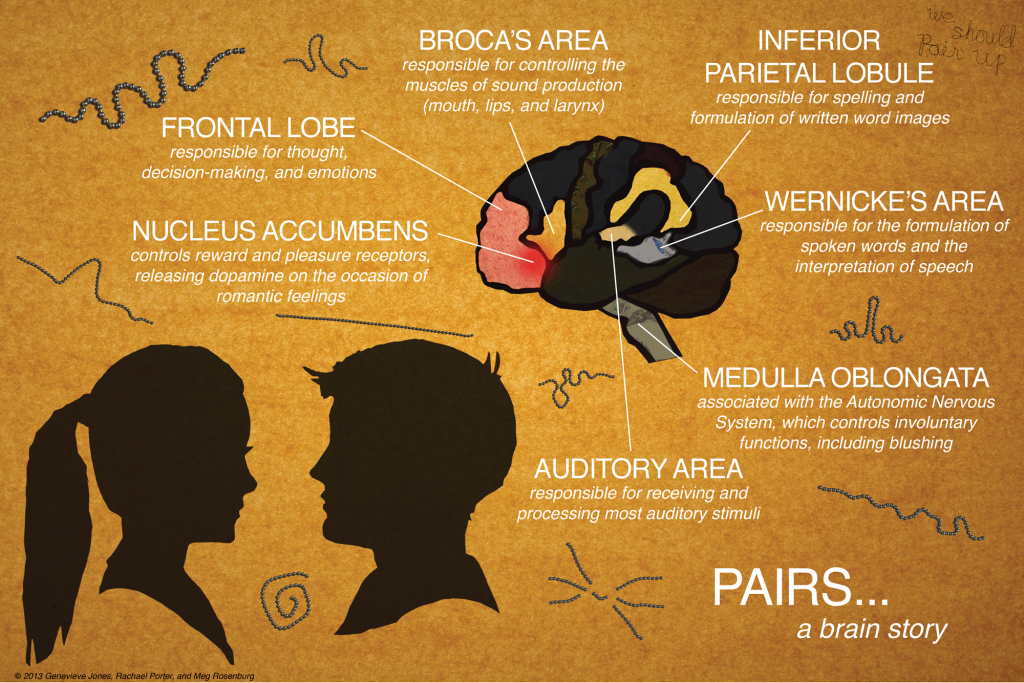
- It’s not really known whether all these regions of the brain in the “language loop” (Wernicke’s Area, Broca’s Area, Inferior Parietal Lobule, etc) are activated one after the other in a sequence or if it’s more like a network, where activating one piece activates everything else all at once.
Ok, that’s it! I learned a lot more about language and the brain than I knew before, and some of it was really unexpected. That, along with getting to work with new awesome collaborators and pushing myself to try new things animation-wise, has made this whole experience worthwhile. Thanks, Joe!
Some sources (these are the ones we came across and read – certainly not the only ones that are relevant!)*:
Academic Papers:
- The effects of homonymy and polysemy on lexical access: an MEG study, by Beretta, Fiorentino, and Poeppel
- Neural response suppression predicts repetition priming of spoken words and pseudowords, by Orfanidou, Marslen-Wilson, and Davis
- On-line orthographic influences on spoken language in a semantic task, by Pattamadilok, Perre, Dufau, Ziegler
- Development of brain mechanisms for processing orthographic and phonologic representations, by Booth, Burman, Meyer, Gitelman, Parrish, and Mesulam
- Lexical representation of phonological variation in spoken word recognition, by Ranbom and Connine
We also made use of a few online resources, especially for visual references to the brain:
- “The Brain from Top to Bottom” at thebrain.mcgill.ca
- “Anatomy and Functional Areas of the Brain”
- “Overview of Addiction Related Brain Regions” describes the role of the nucleus accumbens in the reward circuit.
*Special thanks to Dwayne Godwin for pointing out that last webpage, as well as a few other references to studies on romantic love, pair bonding, and fMRI methods.